Today I check whether the background radiation level correlates with the elevation from sea surface.
I show that the correlation between background radiation level and elevation is about 0.03 (uSv/h per km) and this slope explains only 3% of radiation level variation.
As a data source I use radioactiveathome.org publicly available data.
I use the January 2016 data records for this research. For this single month the data set contains 2,359,151 total records from 299 active sensors all over the world.
Step 1. Obtaining raw data
Each record in the data set contains the following fields: pulses,timespan, lat, lon, sensorID, measurementStartTime
Each record corresponds to the short-time (usually about four minutes) measurement by single sensor.
pulses is the number of pulses regestered with Geiger-Muller counter, timespan is the pulses registration time period, lat is the latitude of the sensor, lon is the longitude of the sensor, sensorID is unique numeric identifier of the sensor and the measurementStartTime identifies the record in time so we can distinguish several measurements of the same sensor.
I get the dataset as a CSV file using the following query
select
max(pulsesCount ) as pulses,
measureTimespanMin as timespan,
lat,
lon,
HostID as sensorID,
timestampUTC as measurementStartTime
INTO OUTFILE '/tmp/radac_jan_2016_qc.csv'
FIELDS TERMINATED BY ',' OPTIONALLY ENCLOSED BY '"'
LINES TERMINATED BY '\n'
from SamplesExt
where timestampUTC>'2016-01-01' AND timestampUTC< '2016-02-01'
AND isExperiment=0 AND quality=0
The result is this file. [wpfilebase tag=file id=12 tpl=download-button /]
Step 2. Calculating background radiation level for each sensor
We assume that the background radiation level for single sensor is the median value of the dose rates across all measurements.
Since there is no median aggregation function available in MySQL, it is calculated in R as well as the rest of the research.
First we load the data
data <- read.csv('radac_jan_2016_qc.csv',sep=',',header = F)
colnames(data) <- c('pulses','timespan','lat','lon','sensorID','mTime')
We calculate the dose rate based on the pulses count and the length of measurement time interval.
(as discussed at radioactive at home forum)
data$doseRate <- (data$pulses/data$timespan)/171.232876
Then, we group the data by the sensors, so we have one record for each sensor. For each sensor we aggregate all records in two ways: dose rate median and number of measurements count.
median_doseRates < - aggregate(doseRate ~ sensorID, data = data , FUN= median)
measurements_counts <- aggregate(pulses ~ sensorID, data = data , FUN= length)
colnames(measurements_counts) <- c('sensorID','measurements')
sensors <- unique(data.frame(data$sensorID,data$lat,data$lon))
colnames(sensors) <- c('sensorID','lat','lon')
sensors <- merge(sensors,median_doseRates)
sensors <- merge(sensors,measurements_counts)
dose rate median is considered to be background radiation level as it eliminates outlier values.
We filter out the sensors that reported too few measurements comparing with others. Thus the median will be only for sensors with lots of measurements.
sensors <- subset(sensors, measurements > 1000)
Step 3. Obtaining elevations for the locations
We use FetchClimate service to obtain the elevations for the locations. In particular, my R script that extracts the data from it.
source('FetchClimate.R')
fetched <- fcTimeSeriesYearly(variable = "elev",
latitude = sensors$lat,
longitude = sensors$lon,
firstYear = 2000,lastYear = 2000)
sensors$elev <- fetched$values
Good. Now we have quality controlled data ready for analysis.
Step 4. Analysing the data
Plotting elevation / dose rate scatter plot reveals that there is one station with much higher radiation dose level.

This is the sensor with ID 12450 located in in Hong Kong owned by the user philip-in-hongkong.
It has 2767 total measurements during the January with the median dose rate level of 1.402946 uSv/h.

This is clearly not the background radiation level whatever causes it! So, let’s remove the station from our data.
sensors <- subset(sensors,sensorID != 12450)
After this we get the following histogram of background radiation level across all sensors all over the world.

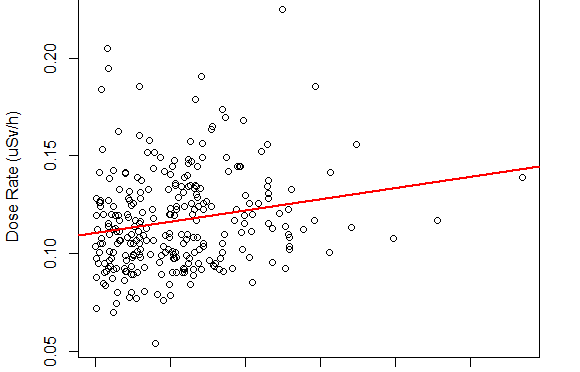
And the doseRate/elev scatter plot is

Linear regression gives that for every kilometer of elevation gain, the dose rate grows for 0.02892 uSv/h
However only 3% of the data variance is explained with linear regression.
lm(formula = doseRate ~ elev, data = sensors)
Residuals:
Min 1Q Median 3Q Max
-0.061040 -0.018112 -0.004224 0.014123 0.100310
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.104e-01 2.357e-03 46.849 < 2e-16 ***
elev 2.892e-05 8.671e-06 3.335 0.000968 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.02461 on 277 degrees of freedom
Multiple R-squared: 0.03861, Adjusted R-squared: 0.03514
F-statistic: 11.12 on 1 and 277 DF, p-value: 0.000968
The R script with analysis is here.
[wpfilebase tag=file id=14 tpl=download-button /]